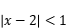 的解集为____________________________________;
的解集为____________________________________;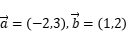 ,求
,求
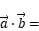 ______________________________ ;
______________________________ ;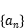 为等比数列,且
为等比数列,且
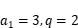 ,求
,求
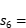 ______________________________ ;
______________________________ ;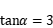 ,求
,求
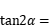 ______________________________ ;
______________________________ ;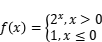 ,则
,则
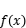 的值域是______________________________ ;
的值域是______________________________ ;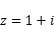 ,则
,则
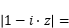 ______________________________ ;
______________________________ ;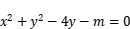 的面积为
的面积为
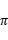 ,求
,求
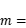 ______________________________ ;
______________________________ ;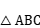 中,
中,
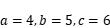 ,求
,求
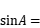 ______________________________ ;
______________________________ ;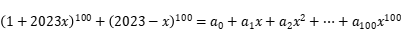 ,其中
,其中
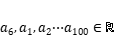 ,若
,若
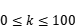 且
且
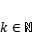 ,当
,当
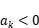 时,
时,
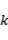 的最大值是______________________________ ;
的最大值是______________________________ ;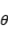 ,斜坡终点距离水平面的垂直高度为4米,游客每走一米消耗的体能为
,斜坡终点距离水平面的垂直高度为4米,游客每走一米消耗的体能为
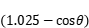 ,要使游客从斜坡底走到斜坡顶端所消耗的总体能最少,则
,要使游客从斜坡底走到斜坡顶端所消耗的总体能最少,则
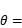 ______________________________ ;
______________________________ ;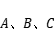 ,满足
,满足
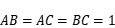 ,在空间内取不同两点(不计顺序),使得这两点与
,在空间内取不同两点(不计顺序),使得这两点与
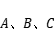 可以组成正四棱锥,求方案数为______________________________ ;
可以组成正四棱锥,求方案数为______________________________ ;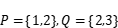 ,若
,若
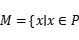 且
且
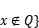 ,则
,则
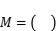 .
.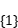
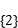
 ,函数
,函数
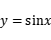 在区间
在区间
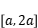 上的最小值为
上的最小值为
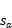 ,在
,在
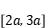 上的最小值为
上的最小值为
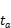 ,当
,当
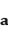 变化时,以下不可能的情形是().
变化时,以下不可能的情形是().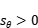 且
且
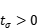
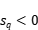 且
且
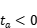
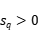 且
且
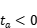
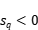 且
且
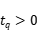
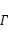 具有如下性质:存在点
具有如下性质:存在点
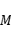 ,使得对于任意点
,使得对于任意点
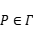 ,都有
,都有
 使得
使得
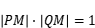 .则称这条曲线为"自相关曲线".判断下列两个命题的真假().
.则称这条曲线为"自相关曲线".判断下列两个命题的真假().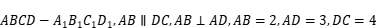 .
.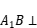 面
面
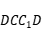
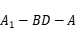 的大小
的大小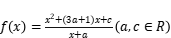
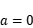 是,是否存在实数
是,是否存在实数
 ,使得
,使得
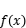 为奇函数
为奇函数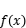 的图像过点
的图像过点
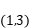 ,且
,且
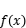 的图像
的图像
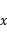 轴负半轴有两个交点求实数
轴负半轴有两个交点求实数
 的取值范围
的取值范围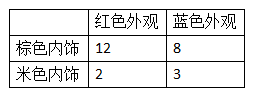
 为小明取到的模型为红色外观,事件B取到模型有棕色内饰
为小明取到的模型为红色外观,事件B取到模型有棕色内饰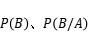 ,并据此判断事件
,并据此判断事件
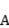 和事件
和事件
 是否独立
是否独立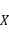 为奖金额,写出
为奖金额,写出
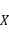 的分布列并求出
的分布列并求出
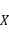 的数学期望
的数学期望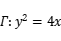 ,第一象限内点
,第一象限内点
 在
在
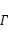 上,
上,
 的纵坐标是
的纵坐标是
 .
. 到准线距离为3,求
到准线距离为3,求
 ;
;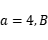 在
在
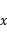 轴上,
轴上,
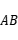 中点在
中点在
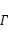 上,求点
上,求点
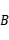 坐标和坐标原点
坐标和坐标原点
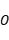 到
到
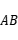 距离;
距离;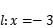 ,令
,令
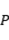 是第一象限
是第一象限
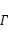 上异于
上异于
 的一点,直线
的一点,直线
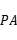 交
交
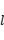 于
于
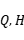 是
是
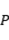 在
在
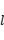 上的投影,若点
上的投影,若点
 满足“对于任意
满足“对于任意
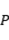 都有
都有
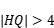 "求
"求
 的取值范围.
的取值范围.
暂无任何记录